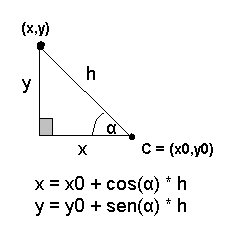Funny Stuff

How to draw a line

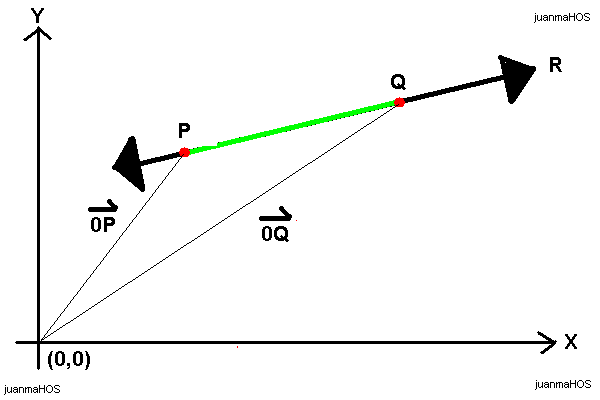
Using linear algebra we can calculate the equation of the R line as follow:

        0P = 0Q + t * v

where:
        P is any point of the line R
        Q is the reference point that defines R
        t * v is the direction vector

Now, we can compute the R equation given two points: (x1,y1) y (x2,y2) as above:

        0Q + t * 0P = (x1,y1) + t ( (x2,y2) - (x1,y1) ) = ( x1 + t (x2-x1), y1 + t (y2-y1) )

        Then:

       x = x1 + t (x2-x1)
       y = y1 + t (y2-y1)

Bingo!, neither X nor Y are restricted by a zero division as happened in y=mx+b.

How to rotate a square

The goal of the algorithm is to draw a square rotated by a theta angle. The point (x0,y0) is the center of the square.

All polygons of side "L" have a radio, in the case of a square, it sizes L/2*sqrt(2).

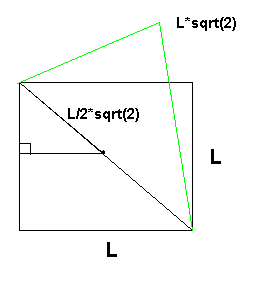
Figure 1.

Using Pitagoras we have that the diagonal D is:

               D² = L² + L², then
               D = sqrt( 2* L² ), then
               D = L * sqrt(2), because D is a side D>0

And the radio is the half of D, then radio = L/2 * sqrt(2).

Now, we know that anyone can draw a point (x,y) using polar coordinates, just what we need is a point C, an angle and a radio (hypotenuse h).

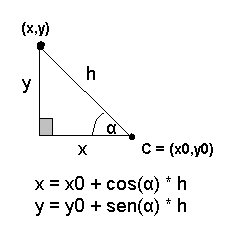
Figure 2.

We can draw a square using four points, four points corresponding to the four radios of the shape, L * sqrt(2):

                line1 = (x1,y1) to (x2,y2)
               line2 = (x2,y2) to (x4,y4)
               line3 = (x4,y4) to (x3,y3)
               line4 = (x3,y3) to (x1,y1)

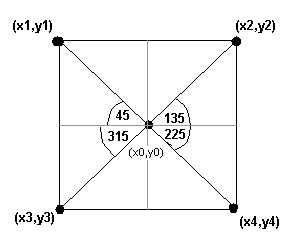
Figure 3.

We can use the polar coordinates to find the points of the square where (x0,y0) is the center and L/2 * sqrt(2) is the size of the hypotenuse. To rotate the square theta grades just add theta grades to alpha. The equation is above:

               x = x0 + cos(alfa+theta) * L* sqrt(2)
               y = y0 + sen(alfa+theta) * L * sqrt(2)

                where alfa: 45,135,225 and 315

It is the algorithm, special thanks to the Linear Algebra.